Divisioni in colonna a più cifre con resto

Dopo aver imparato a calcolare le divisioni semplici ad una cifra, eccoci pronti per un argomento più difficile, le divisioni in colonna a più cifre con resto.

Passiamo ad un metodo "in colonna" perché in questo modo sarà più facile risolvere anche operazioni che sembrano complicate.

Prima, però, diamo qualche definizione.

Sommario

• Le divisioni, cosa sono
• Proprietà nelle divisioni
• Come si calcolano le divisioni in colonna

Cosa sono le divisioni, definizioni

Le divisioni sono formate da

• DIVIDENDO
• DIVISORE
• QUOZIENTE
• RESTO

Ad esempio, nella divisione 16 : 5

• Abbiamo il dividendo che è 16
• Il divisore (cioè il numero che divide) che è 5
• Mentre, il risultato, chiamato quoziente, è 3 perché sedici diviso cinque fa tre.
• Non è tutto: il risultato non è "esatto", dalla divisione avanziamo qualcosa, un numero: 1
  Ecco, 1 è il resto

Quindi, riassumendo:

16 : 5 = 3 con resto 1

Dividendo : Divisore = Quoziente con Resto

Regole, proprietà nelle divisioni

Vediamo due piccole regole:

1. Una prima proprietà che possiamo subito imparare è che il resto non potrà mai essere maggiore del divisore.
2. Una seconda proprietà è che il Dividendo sarà uguale al prodotto tra Divisore e Quoziente, più il resto:

5 x 3 = 15 --- > 15 + 1 = 16

(Divisore x Quoziente) + Resto = Dividendo

Diciamo che questa seconda regola potrà essere utile come prova di verifica: facciamo il calcolo inverso per vedere se è giusta la divisione.

Come si calcolano le divisioni in colonna

Ora possiamo andare avanti e iniziare a capire meglio le divisioni in colonna.

La forma in cui si presentano è questa:

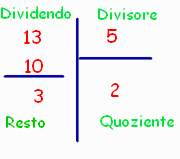
Qui ci fermiamo con il calcolo perché il 3 (resto) è più piccolo del 5 (divisore). Questo vuol dire che non possiamo continuare a dividere per 5.

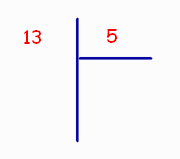
Come vedete abbiamo il Dividendo a sinistra e il Divisore a destra, separati da due linee.

Esercizio 1

Il primo calcolo da fare è questo: quante volte il 5 sta nel 13?
Esatto, 2 volte, quindi scriviamo "2" sotto il "5", cioè nello spazio che useremo per il Quoziente:

A questo punto moltiplichiamo il quoziente ("2") per il Divisore ("5") e otteniamo un "10", che scriveremo sotto il Dividendo ("13").

La colonna a sinistra la usiamo per fare le sottrazioni e calcolare il resto.
Come vedete qui sotto abbiamo che 13 - 10 = 3:


Il risultato finale della divisione 13 : 5 è 2 con il resto di 3.

Esercizio 2

Ora, un esercizio un po' più difficile.
Quanto fa 340 : 13 ?

In questo esempio non dobbiamo calcolare subito quante volte il 13 sta nel 340.
Grazie alle divisioni in colonna, possiamo iniziare dal 34, cioè le prime due cifre a sinistra del 340.
In pratica mettiamo un attimo da parte lo "0" e cerchiamo di capire se il 34 è divisibile per 13.

Quante volte il 13 sta nel 34?

Giusto, 2 volte, perché il 3 sarebbe troppo (infatti, facendo la prova inversa vista prima, 13 x 3 fa 39, un numero maggiore del nostro 34.

Il quoziente moltiplicato per il divisore non deve dare un risultato maggiore del dividendo).

Quindi, scriviamo:

Come vedete, abbiamo considerato il 34 disegnando sopra una specie di cappello curvo.
Abbiamo visto che il 13 sta nel 34 per 2 volte, quindi abbiamo scritto il "2" nello spazio del quoziente.

Poi abbiamo moltiplicato il 13 (divisore) per 2 (quoziente) ottenendo il "26", che, come prima, andiamo a scrivere nella colonna di sinistra, proprio sotto il dividendo.

Facciamo poi la sottrazione tra 34 e 26 e il risultato è 8.

A questo punto abbiamo finito? Certo che no! Ci manca lo "0" di prima che avevamo messo un momento da parte.

Nelle divisioni a colonna, dopo aver fatto i calcoli sulle prime cifre del dividendo (nel nostro caso il 34) si possono usare le altre cifre, una alla volta (nel nostro caso lo 0 ).

Lo zero viene portato giù, abbassato, di fianco al risultato della sottrazione risolta prima, cioè di fianco al nostro "8".

Per ricordarci di aver abbassato lo "0", ci disegniamo sopra una specie di accento (vedi sopra), così non lo useremo un'altra volta.

Ora, abbassando lo 0 vicino all'8, abbiamo un nuovo numero: 80.

Adesso ripetiamo le operazioni di prima. Verifichiamo quante volte il 13 sta nell'80.

La risposta è 6. Il tredici sta sei volte nell'ottanta.
Facendo il calcolo inverso, cioè 13 x 6, otteniamo 78.

Quindi, scriveremo il 6 nello spazio del quoziente, vicino al 2.
Poi scriveremo il 78 nella colonna di sinistra, sotto l'80.

Come vedete sopra, abbiamo anche calcolato la sottrazione 80-78 che fa 2.

Non possiamo più continuare con i calcoli, perché non abbiamo più cifre da abbassare e il 2 non è divisibile per 13.
Quindi, il risultato finale è 26 (quoziente) con il resto di 2.

Esercizio 3

Terzo esercizio ancora più difficile.

2890 : 25

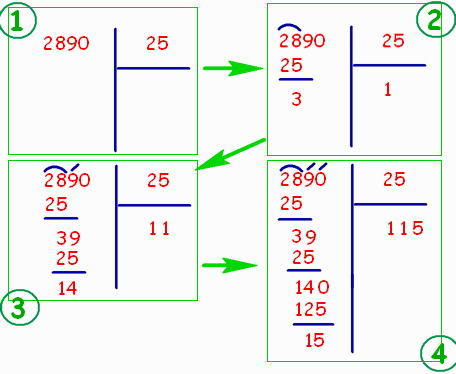
Qui sopra abbiamo quattro passaggi.

1. Nel primo abbiamo la divisione di partenza
2. Nel secondo, prendendo le prime cifre a sinistra del dividendo, cioè 28, vediamo subito che il nostro divisore, cioè 25, sta una sola volta nel 28, quindi nel quoziente scriviamo 1. Dato che 1 x 25 = 25, scriviamo 25 sotto il 28 e dalla sottrazione abbiamo un 3
3. Nel terzo passaggio abbassiamo il 9 vicino al 3 a otteniamo un 39. Il 25 nel 39 sta una volta sola, perciò scriviamo un altro 1 nel quoziente, vicino all'altro 1. Dato che 1 x 25 = 25, scriviamo 25 sotto il 39 e dalla sottrazione (39-25) abbiamo un 14
4. Nell'ultimo passaggio abbassiamo l'ultima cifra del dividendo, cioè lo "0" e lo mettiamo vicino al 14, ottenendo 140. Il 25 sta 5 volte nel 140, quindi scriviamo 5 nello spazio quoziente, vicino all'11 calcolato prima, in modo da avere 115. Dato che 5 x 25 = 125, scriviamo 125 sotto il 140 e dalla sottrazione (140-125) abbiamo 15.

Alla fine, non avendo più cifre da abbassare e dato che il 15 avanzato non è divisibile per 25, possiamo dire di aver finito il calcolo.

• 2890 : 25 = 115 con resto di 15

Facciamo la prova inversa, al contrario, per vedere se il calcolo è giusto. Ricordate che dobbiamo moltiplicare il quoziente per il divisore e poi sommare il resto:

• 115 x 25 = 2875
• 2875 + 15 = 2890

Perfetto! Con la prova inversa abbiamo come risultato 2890, cioè il dividendo. Quindi la divisione è stata calcolata in modo giusto.