Come si fa la "Prova del Nove" nelle moltiplicazioni

Prima di andare avanti dobbiamo rispondere ad una domanda: avete capito come si fa la Prova del Nove nelle addizioni?

Se la risposta è "No", allora seguite il relativo collegamento blu.
Altrimenti possiamo passare di livello e spiegare un altro "trucco" matematico, quello che ci aiuta a verificare il risultato nelle moltiplicazioni.

Si chiama sempre Prova del Nove, perché tutti i numeri che calcoleremo arrivano massimo fino a 9.
Ovviamente, come le altre volte, partiamo prima con esercizi svolti, esempi, più facili e semplici.

Prendiamo una moltiplicazione a caso. Che ne dite di.. 12 x 12 ? Ok, andata!

Dodici per dodici (numeri definiti "fattori") dà come risultato 144 (che in caso di moltiplicazioni si chiama "prodotto").

12 x 12 = 144

Siamo sicuri che sia giusto? Sì, no, forse?

Utilizziamo la Prova del Nove, mettendo l'operazione in colonna (se non vi sentite pronti e volete ripassarle, leggete la pagina: moltiplicazioni in colonna, e poi tornate qui).

12 x
12 =
144

Come abbiamo già visto nelle addizioni, il trucco è quello di trasformare tutti i numeri a due, tre o più cifre in numeri ad una cifra.
Per farlo, sommiamo tra loro le cifre che compongono il numero.

Ad esempio, per trasformare il 12 facciamo 1+2 che fa 3 e ci prendiamo il 3 per la prova del nove.
Mentre, per quanto riguarda il prodotto, 144, facendo la somma 1+4+4 otteniamo 9.

Date un'occhiata allo schema qui sotto:

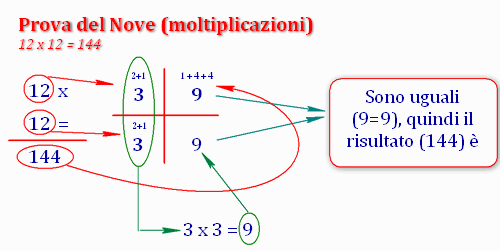
Come vedete, di fianco alla moltiplicazione abbiamo messo una specie di croce con quattro quadranti.

Nella prima colonna abbiamo messo i fattori "trasformati" (12 e 12 che diventano 3 e 3).
Nel terzo quadrante, in alto a destra, abbiamo messo il prodotto "trasformato" (144 che diventa 9).

A questo punto, per fare la verifica, dobbiamo moltiplicare, tra loro, i numeri presenti nella prima colonna (nel nostro caso 3 x 3). Il risultato (9) dev'essere uguale al numero già calcolato nel terzo quadrante, in alto a destra (9).

9 = 9... giusto!

Proviamo con un esercizio più difficile: 56 x 39, che è uguale a 2184.
Passiamo subito allo schema:

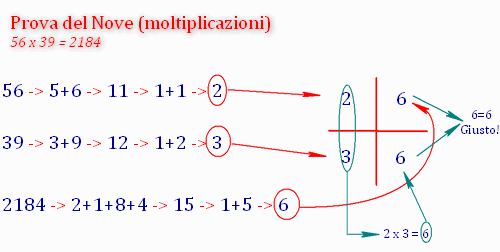
Tutto giusto! L'importante è che i numeri nella seconda colonna (6 e 6 in questo caso) siano uguali.

Qui sotto trovate uno schema riassuntivo, con i vari quadranti (chiamati Q1, Q2, Q3 e Q4):

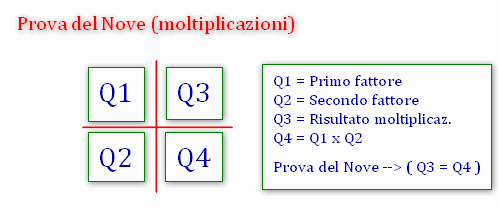
Chiaro? Speriamo di sì. In caso contrario basterà rileggere questa pagina dall'inizio e provare a fare qualche esercizio inventando dei numeri da moltiplicare tra loro.