Partiamo subito dalla definizione:
Con x e y, variabili reali, si dice che y è una funzione di x quando ad ogni valore della x corrisponde uno ed un solo valore della y.
y = f (x)
che si può anche scrivere come
f : x --> y
Bene. Ottimo inizio. Ma, alla fine, che cosa sono le funzioni? A cosa servono in pratica? Come si risolvono?
Giuste osservazioni, andiamo sul concreto e cerchiamo di capire il loro importante compito.
Prendiamo come esempio due insiemi A e B.
- L'insieme A è formato da nomi di persona: Luca, Marco, Giulia, Anna.
- L'insieme B è formato da nomi di sport: Calcio, Basket, Pallavolo, Nuoto, Baseball.
Noi sappiamo che ogni persona pratica un solo sport e quello soltanto.
A Luca piace il calcio, a Marco il basket, Giulia gioca a pallavolo, mentre Anna nuota in piscina, ma nessuno di loro pratica il baseball.
Graficamente i due insiemi saranno così rappresentati:
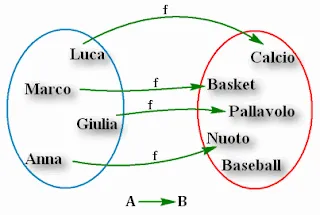
Come vedete, ad ogni elemento dell'insieme A corrisponde un elemento dell'insieme B.
Vi è una relazione tra i due insiemi:
x pratica (come sport) yQuesto tipo di relazione viene definita come "Funzione".
Proprietà delle funzioni
Quindi, la relazione tra A e B si dice funzione se, ad ogni elemento di A corrisponde uno, ed uno soltanto, elemento di B. Tale relazione viene anche detta "Corrispondenza univoca".
"A" viene chiamato "dominio" della funzione, mentre il sottoinsieme di "B", formato solo dagli sport praticati (calcio, basket, pallavolo e nuoto) e non dagli altri (baseball) che non hanno corrispondenze con "A", viene detto "codominio", e lo indichiamo con la lettera "C".
Riassumendo abbiamo:
- Insieme A: Luca, Marco, Giulia, Anna
- Insieme B: Calcio, Basket, Pallavolo, Nuoto e Baseball
- Sottoinsieme C (di B): Calcio, Basket, Pallavolo, Nuoto
Il resto di B (in questo caso, il baseball) non ci interessa.
Quindi, per logica, "C" può essere, in generale, minore o uguale a "B".
Se nell'esempio sopra avessimo avuto un altro tipo di relazione (Luca che pratica sia calcio che basket oppure Giulia che non pratica alcuno sport), allora non esisterebbe una funzione.
La funzione esiste se "ogni" (quindi, tutti) elemento di A è associato ad uno (ed uno soltanto) elemento di B.
Tuttavia, l'insieme B può anche avere elementi che non trovano corrispondenza con altri elementi di A (nel nostro esempio, il baseball). In tale casa la funzione può ugualmente esistere.
La "Funzione" viene rappresentata con la lettera "f" minuscola (vedi grafico sopra, le frecce verdi):
f : A --> B
"f è una funzione da A a B"Per indicare che ad ogni elemento di A (definito con la variabile x) corrisponde un elemento di B (definito con la variabile y), possiamo scrivere la funzione in questo modo:
f : x --> y
con la funzione "f", "y" è l'immagine di "x"Una delle forme più conosciute per rappresentare una funzione è questa:
y = f (x)
"y è una funzione di x"Esempio, esercizio pratico di funzione
Supponiamo di avere un gruppo di ragazze e un gruppo di ragazzi, che hanno una relazione basata su altezza ed età. Le altezze in centimetri variano a seconda dell'età e del genere.
Le età, per tutti e due i gruppi, sono: 10, 15, 20 anni.
Mentre le altezze, per ogni età, sono:
- 130, 160, 175 (ragazze)
- 135, 165, 180 (ragazzi).
Come potete notare, per ogni età, il ragazzo è più alto della ragazza di 5 centimetri.
Se volessimo scrivere la relazione tra le altezze, quindi una funzione, come sarebbe?
Definendo con y le altezze maschili e con x le altezze femminili, avremmo che:
y = x + 5Infatti, se provate, per ogni età, a sostituire al posto di "x" le età delle ragazze (130, 160, 175) otterrete, grazie alla somma "+5" le età dei ragazzi (135, 165, 180).
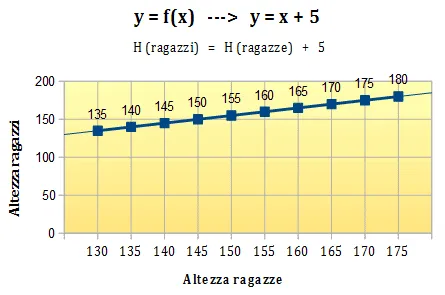
Nel grafico qui sopra abbiamo inserito sull'asse x (orizzontale) i dati "Altezza ragazze" e sull'asse y (verticale) i dati "Altezza ragazzi". La linea che unisce i dati è la nostra funzione (y = x + 5) rappresentata graficamente. Come potete notare, si tratta di una retta.
Grazie alla funzione possiamo dunque calcolare altri dati. Ad esempio, se a 12 anni le ragazze sono alte 145 centimetri, sapendo che (y = x + 5), allora possiamo subito verificare che i ragazzi, sempre a 12 anni, sono alti 150 centimetri. E così via, variando l'altezza femminile si trova automaticamente quella maschile, prendendo in considerazione i due insiemi per i quali vale la nostra funzione.
Ecco un esempio pratico dell'utilità delle funzioni. Conoscendo un insieme di dati x e sapendo che tipo di relazione vi è tra i due insiemi, possiamo calcolare i dati y.
Classificazione delle funzioni
Le funzioni possono essere di diversi tipi.
Funzioni algebriche
- razionali (intere o fratte)
- irrazionali (intere o fratte)
Funzioni trascendenti
- esponenziali
- logaritmiche
- goniometriche
