Il triangolo è formato da tre lati (che possono avere lunghezze uguali o diverse tra loro) e tre angoli (con inclinazioni uguali o diverse). Studiando il quadrato e il rettangolo, invece, abbiamo notato che gli angoli hanno tutti la stessa inclinazione, cioè 90°.
Nella figura piana che trattiamo in questa pagina, in base alla lunghezza dei lati e dal tipo di angolo, possiamo distinguere vari tipi di triangoli, che dopo vedremo.
Prima, però, cerchiamo di capire come si calcola il perimetro.
Se cerchi una versione adatta ai bambini della scuola elementare leggi quest'altra pagina: Tipi di triangolo e perimetro.
Sommario
Come calcolare il perimetro del triangolo
Il perimetro di un triangolo è la misura totale dei tre lati, la somma dei tre segmenti che formano la figura.

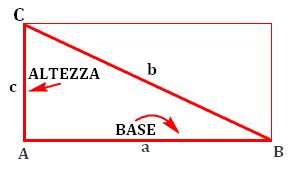
Ad ogni angolo c'è una lettera, per distinguere i tre vertici del triangolo: A, B, C.
Tra A e B notiamo la lettera (minuscola) "a" che indica la misura del lato che va da A a B (segmento AB). Stesso discorso per "b" (BC) e "c" (AC).
Dati i tre lati AB, BC e AC, abbiamo che:
PERIMETRO DEL TRIANGOLO = AB + BC + AC
Ricordando che il segmento AB misura "a", il segmento BC misura "b" e il segmento AC misura "c", possiamo anche scrivere che:
PERIMETRO DEL TRIANGOLO = a + b + c
Un esempio potrebbe chiarire meglio la formula.
Supponiamo di avere un triangolo ABC (come quello in figura) con i lati:
"a" = 10
"b" = 7
"c" = 5
Quanto sarà il perimetro?
PERIMETRO DEL TRIANGOLO = a + b + c = 10 + 7 + 5 = 22
In pratica si fa solo la somma dei tre lati. Facile, no?
Come calcolare l'area del triangolo
Dopo aver capito come trovare il perimetro, passiamo ora a spiegare il calcolo dell'area del triangolo.
Con il perimetro guardiamo solo le lunghezze dei lati.
Con l'area, invece, calcoliamo tutto il contenuto del triangolo. Guarda la figura:

Per calcolare l'intera area abbiamo bisogno di alcuni dati importanti.
Uno è la misura della base. In questo caso prendiamo il segmento AB.
L'altro è la misura dell'altezza del triangolo, a partire dalla base.
Per iniziare, utilizziamo un triangolo semplice, quello che si ottiene dividendo in due parti un rettangolo, tracciando una diagonale:
Come vedete in figura, il nostro triangolo non è altro che metà rettangolo.
Questa osservazione ci aiuta molto!
Infatti, per calcolare l'area del triangolo, basterà calcolare l'area del rettangolo (se non vi ricordate, provate a leggere "Come calcolare l'area del rettangolo".) e poi dividere per due.
Più facile di così.. .
Quindi, osservando che la base del triangolo è uguale al segmento AB (che misura "a") e che l'altezza è uguale al segmento AC (che misura "c"), possiamo calcolare l'area in questo modo:
AREA DEL TRIANGOLO = (BASE x ALTEZZA) / 2
AREA DEL TRIANGOLO = (a x c) / 2
L'area del rettangolo sarebbe "lato lungo per lato corto", cioè, in figura, base per altezza.
Avendo però sottolineato che il nostro triangolo è esattamente la metà del rettangolo, allora dividendo per due otteniamo l'area del triangolo.
Esempio
Se la base è pari a 10 e l'altezza è pari a 5, l'area sarà:
AREA = (10 x 5) / 2 = 50 / 2 = 25
Ecco qui. Facilissimo.
L'area del triangolo è uguale alla BASE moltiplicata per l'ALTEZZA, il tutto diviso per due.
In generale l'altezza viene definita con la lettera "h".
Formula del perimetro e dell'area del triangolo
Perimetro = lato + lato + lato = a + b + c
Area = (base x altezza) / 2
Tipi di triangolo
Il triangolo può essere:
Andiamo per ordine.
Ricordando che la somma di tutti gli angoli dei triangoli (qualsiasi forma abbiano) deve misurare 180°.
Il TRIANGOLO RETTANGOLO è abbastanza semplice.
Quello visto prima, per calcolare l'area, fa parte di questa tipologia.
Si riconosce dal fatto che ha un angolo di 90°, cioè retto (per questo si chiama "rettangolo").
Può avere due lati uguali: ad esempio, se dividiamo un quadrato in due, tracciando una diagonale da un angolo a quello opposto (in figura sotto, da B a D), otteniamo due triangoli rettangoli con due lati uguali per ciascuno.

Come potete notare, dal quadrato ABCD (qui sopra disegnato), tracciando la diagonale "i", abbiamo creato due triangoli rettangoli: ABD e BCD.
Tutti e due hanno un angolo di 90° (in A e in C) e due angoli di 45° (in B e in D). Questi ultimi sono esattamente la metà di 90°, grazie alla perfetta divisione ottenuta con la diagonale.
Tutti e due i triangoli hanno due lati uguali (AB e AD nel primo e BC e CD nel secondo).
Anche dal rettangolo, però, si possono avere, tracciando una diagonale, due triangoli rettangoli. L'unica differenza è che non hanno due lati uguali ma tutti diversi. Vediamo il disegno qui sotto.

Abbiamo il triangolo rettangolo 1 (ABD) e il triangolo rettangolo 2 (BCD).
Tutti e due hanno un angolo retto (il primo in A, il secondo in C).
Gli altri angoli possono avere inclinazioni diverse (dipende da quanto sono lunghi i lati AB e AD nel primo e BC e CD nel secondo).
Un esempio di triangolo rettangolo è dunque questo:
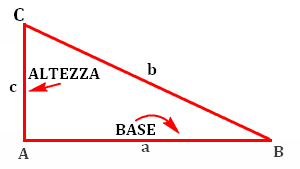
Il perimetro del triangolo rettangolo si calcola con la formula generale:
P = a + b + c (cioè AB + BC + AC)
Anche per l'area rimane valida la solita formula:
A = (base x altezza) / 2 = (a x c) / 2
Il TRIANGOLO EQUILATERO lo si riconosce perché ha tutti e tre i lati uguali, della stessa lunghezza. Questo porta, inoltre, ad avere anche tutti gli angoli uguali, di 60° (la somma dà sempre 180°).

Questo triangolo equilatero (in figura) ha tre lati uguali, che misurano tutti "a".
Quindi AB = BC = AC.
Dividendo la base "a", esattamente a metà (diviso due), otteniamo due triangoli rettangoli (visti prima) con lati: "a", "a/2" e "h".
Il perimetro del triangolo equilatero, che come sappiamo si calcola facendo la somma dei tre lati, si può anche scrivere con la formula:
P = (3 x a), cioè il lato moltiplicato per tre (dato che son tutti uguali).
L'area è sempre "base per altezza diviso due".
Il TRIANGOLO ISOSCELE è un triangolo equilatero "allungato". Infatti ha una base e due lati uguali tra loro ma di misura differente rispetto alla base.
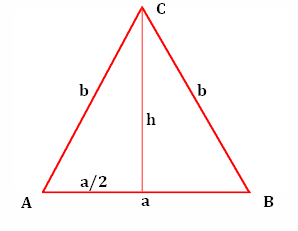
Qui abbiamo una base "a" e due lati obliqui "b", uguali tra loro (BC = AC).
Dividendo a metà la base (con il segmento che misura h) abbiamo di nuovo i due triangoli rettangoli.
La formula del perimetro del triangolo isoscele, con una base e due lati uguali, si può scrivere così:
P = (a + 2b).
L'area si calcola come negli altri triangoli A = (base x altezza)/2.
Infine, abbiamo il TRIANGOLO SCALENO.

Questa figura è formata da tre lati diversi (a, b, c), ognuno con misura differente. Inoltre, anche tutti gli angoli (in A, in B e in C) sono diversi tra loro.
A differenza del triangolo rettangolo, qui non esiste un angolo retto.
La formula per il perimetro è quella generale: P = a + b + c.
Così come quella per l'area: A = (base x altezza) / 2 = (a x h) /2.
Esercizi sui triangoli
Problemi con soluzioni
1) Se ho un triangolo rettangolo che ha i seguenti lati: a = 3 ; b = 6 ; c = 4
Quanto sarà il perimetro? E l'area?
- P = 3 + 6 + 4 = 13
- A = (base x altezza) / 2 = (3 x 4) / 2 = 6
Quanto sarà il perimetro? E l'area?
- P = (3 x a) = 3 x 6 = 18
- A = (base x altezza) / 2 = (6 x 3) / 2 = 9
Problema più complicato
3) Se ho un triangolo isoscele che ha la base a = 8, i due lati obliqui b = 12
Quanto sarà il perimetro? E l'area?
- P = a + (2 x b) = 8 + (2 x 12) = 32
L'altezza si calcola così:
area del quadrato costruito sull'altezza = area del quadrato costruito sull'ipotenusa (il lato più lungo, quindi "b") - area del quadrato costruito sul cateto (il lato più corto, quindi "a/2": la metà di "a", perché, come puoi vedere nella figura, sopra, del triangolo isoscele, a noi interessa il triangolo formato da "b", "h" e "a/2", cioè la metà del triangolo)
(h x h) = (b x b) - (a/2 x a/2)
dato che a = 8, allora a/2 = 4
(h x h) = (12 x 12) - (4 x 4) = 144 - 16 = 128
altezza per altezza = 128
per calcolare solo "h", devo fare la radice quadrata di 128, cioè h = 11,3 (circa)
Ora, tornando alla nostra formula dell'area,
- A = (base x altezza) / 2 = (a x h) / 2 = (8 x 11,3) / 2 = (90,4) / 2 = 45,2
Conclusione
Insomma, come potete subito capire, qualsiasi sia il tipo di triangolo, le formule per calcolare il perimetro e l'area sono le stesse. L'importante è avere i dati: la misura dei lati e, dove richiesta l'area, anche la misura dell'altezza.
Se vuoi approfondire l'argomento, magari facendo uso di quanto imparato con triangolo e quadrato, potresti leggere la pagina sul Teorema di Pitagora, uno dei più famosi e interessanti.


Nessun commento:
Posta un commento
Scrivi un commento qui sotto